求二进制数中1的个数

编程之美第2.1题————求二进制数中1的个数

题目描述：对于一个字节（8bit）的无符号整形变量，求其中的二进制表示中“1”的个数，要求算法的执行效率尽可能的高。

书中由浅入深地给出了几种解法。

解法一

也是最容易想到的，因为对于无符号整数，若采取对2取余操作，结果只有两种，奇数余1，偶数余0，而奇数的二进制最后一位为1，偶数的二进制最后一位为0。这样我们就可以通过奇偶判断来得到结果，以二进制数1011和1100举例：

1011 对2取余，余数为1，二进制末尾为1，即含有一个1

1100 对2取余，余数为0，二进制末尾为0，即含有一个0

不管这个二进制数的高位有多少个0或者多少个1，对2取余的操作只与最低位相关。所以，如果能够把所有的位都作为最低位，对2取余一次，然后将结果相加，即可得到该题答案。而二进制数中，右移操作，就相当于除以2，所以有了以下解法。

[c]
unsigned int Count (unsigned int x)
{
unsigned int num = 0; // the result
while(x) // end of loop when x is 0
{
if(x % 2 == 1) // to judge whether the last bit is ‘1’
{
num++;
}
x = x / 2; // same as x >> 1
}
return num;
}
[/c]

当然你要是觉得除法耗费时间，可以把x = x / 2改成 x >> 1，本质上是一样的。

解法二

既然提到了右移，就能想到，右移的时候会把最后一位移丢，那我们只要在每一次移动的时候，判断一下最后一位是否为1，然后重复该步骤直到将所有位都移除。用1011举例：
1011，最后一位是1，结果加1，右移一位，变成0101

0101，最后一位是1，结果加1，右移一位，变成0010,

0010，最后一位是0，结果不加，右移一位，变成0001，

0001，最后移位是1，结果加1，右移一位，变成0000，所有位都已移除，结束算法。

而判断最后一位是否为1，可以用&操作，x & 0x1 即可。

算法如下：

[cpp]
unsigned int Count2 (unsigned int x)
{
unsigned int num = 0; // the result
while(x) // end the loop when x is 0
{
// x & 0x01 will be 0 if the last bit is ‘0’, otherwise ‘1’
num = num + (x & 0x01);
x = x >> 1; // right shift 1 bit
}
return num;
}
[/cpp]

可以看到，上述两种解法对每一位都进行了比较运算，时间复杂度都为O(log₂^x)，出于降低时间复杂度的角度，书中又给出了第三种解法，让复杂度只与二进制数中‘1’的个数相关。

解法三

该解法确实好玩儿，让我有一种“让广大码农飞，让搞算法的死”的感觉，很巧妙。还是先举一个例子来阐述原理：对于无符号一个二进制数x，与 x – 1 采取&操作会消除x最低位的1，假设x为1010,0000：

x – 1 的二进制为 1001,1111，与x进行&以后得1000,0000，最低位的1没有了，让x = 1000,0000

x – 1 的二进制位 0111,1111，与x进行&作以后得0000,0000，最低位的1没有了，x 为0，结束算法

算法一共就执行了两次，即‘1’的个数。不管‘1’之后有多少个0，x & (x – 1) 总是会消除最低位的1，这就是该算法的巧妙之处了。代码如下。

[cpp]
unsigned int Count3 (unsigned int x)
{
unsigned int num = 0;
while(x)
{
x = x & (x – 1);
num++
}
return num;
}
[/cpp]

算法把时间复杂度降到了O(n)，n为二进制中‘1’的个数。应该算是很不错了，关键是很巧妙，灰常好玩儿有木有。

书中还给出了查表法，因为题目是八位的二进制，那么一共也才256个数，完全可以开一个256大小的数组，将结果存起来，如255的二进制为1111,1111，让result[255] = 8，同理把其他所有数的结果都存一遍，以后需要的时候直接返回result[x]就可以了。只是如果不是八位的，变成了32位，那查表这种空间换时间的方法就很不划算了。

后来查阅网上一些题解的时候，发现很多大牛对此题书中解法的提出了质疑。比如解法三，虽然理论上一次地址计算就可以解决，但实际上这里用到一个访存操作，且第一次访存的时候很有可能那个数组不在cache里，这样一个cache miss导致的后果可能就是耗去几十甚至上百个时钟周期（因为要访问内存）。而对于这种数据规模给定，而且很小的情况下，耗去几十甚至上百个时钟周期是很慢的。所以对于这种“小操作”，这个算法的性能其实是很差的。

然后我看到了另外一个巧妙的解法，有点像二分，个人灰常喜欢。

解法X

怎么说呢，先举个例子，比如整数212的二进制1101,0100，一共有4个‘1’对吧。而正好又是8位大小，有没有一种“对折对折再对折”的冲动，有木有？

于是算法可以这样描述：

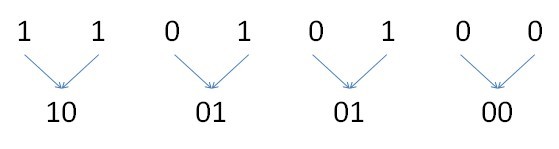
先把相邻的‘1’的个数算出来，同样二进制的形势保存起来

那么现在 10,01,01,00分别代表了1101,0100中相邻两位中‘1’的个数。而且由于是计算的相邻两位，所以‘1’的个数最多为2，所以用两位足够表示。

现在的问题变成了，如何继续处理第一步得到的结果1001,0100呢，对于1001,0100，

第8位，第7位联合起来,即10，表示了原二进制数（1101,0100）中第8位与第7位所含‘1’的个数。

第6位，第5位联合起来,即01，表示了原二进制数（1101,0100）中第6位与第5位所含‘1’的个数。

第4位，第3位联合起来,即01，表示了原二进制数（1101,0100）中第4位与第3位所含‘1’的个数。

第2位，第1位联合起来,即01，表示了原二进制数（1101,0100）中第2位与第1位所含‘1’的个数。

现在我们就需要把新得到的二进制串1001,0100的

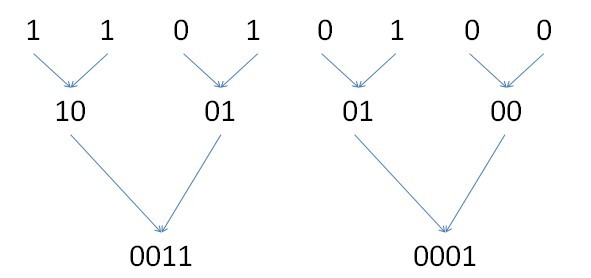
8、7联合位与6、5联合位相加，即把10和01相加，代表原第8,7,6,5位的‘1’的个数

（因为8、7联合起来才表示原第8位和原第7位一共有多少个‘1’，这里不能再次分开计算他们了，应该把他们当成一个整体。同理6、5位，也当成一个整体来看待）

4、3联合位与2、1联合位相加，即把01和01相加，代表原第4,3,2,1位的‘1’的个数

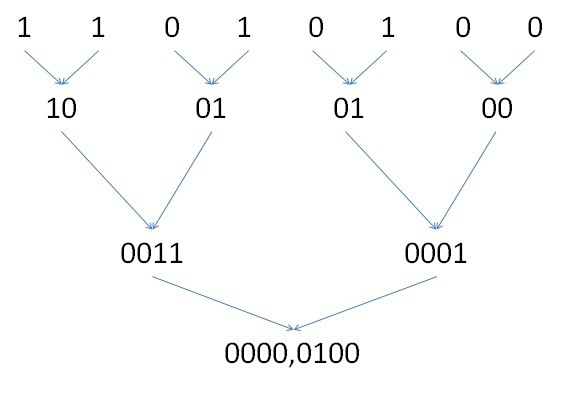
后面就类似啦，把0011与0001相加，代表原第8,7,6,5,4,3,2,1位的‘1’的个数

就得到最后的结果了，结果为4。

好了，现在剩下的问题就是怎么样让相邻的位相加，怎么样让相邻两位的相加，怎么样让相邻四位的相加。

拿相邻两位的相加举例，

(x & 0x55) + (x >> 1  & 0x55)

因为0x55展开成二进制就是0101,0101，观察1的位置，奇数位为1，偶数位为0，这样和x进行与操作的结果就是保留了x的奇数位。然后x右移一位以后，再与0x55进行与操作，对x>>1来说是保留了奇数位，但相对于原来的x则是保留了偶数位。最后将两式相加，就得到了x的二进制中，相邻两位的‘1’的个数。

同理因为0x33展开成二进制是0011,0011，所以相邻二位的相加则为

(x & 0x33) + (x >> 2 &  0x33)

因为0x0f展开成二进制是0000,1111，所以相邻四位的相加则为

(x & 0x0f) + (x >> 4 &  0x0f)

所以算法如下：

[cpp]
unsigned int CountX (unsigned int x)
{
x = (x & 0x55) + (x >> 1 & 0x55);
x = (x & 0x33) + (x >> 2 & 0x33);
x = (x & 0x0f) + (x >> 4 & 0x0f);
return x;
}
[/cpp]

优美的代码总是很简洁，这个算法估计只要十几行指令吧，速度应该是很不错了，至于网上其他更好的算法，写得让我半天看不懂哈哈~~感觉太复杂了也就失去了美。

最后，POJ的相关题目有Problem2453

原题链接：http://poj.org/problem?id=2453

解题报告：http://keping.me/poj2453/

That’s all,

Enjoy!